CASO 1
Cuando a, b, c, d, e son diferentes entre sí
Usa el interactivo
-
Arrastra las piezas haciendo clic sostenido sobre ellas.
-
Activa la casilla para rotar y desliza el vértice blanco.
-
Activa al casilla del color de la pieza que desee voltear.
EDUCACIÓN MEDIA SUPERIOR
-
Realice la construcción del tangrama usando hojas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
Reproduzca cada una de las 6 figuras faltantes que se muestran en fondo azul.
-
En plenaria, pida a los estudiantes que argumenten si el perímetro o el área cambia de una a otra de las 11 figuras posibles.
-
Solicite que a partir de las medidas esablecidas, expresen el área y perímetor de cada figura posible. (La solución se muestra en la siguiente imagen)
COMO USARLO EN EL AULA
EDUCACIÓN PRIMARIA
-
Realice la construcción del tangrama usando hojas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
Pida a los estudiantes que reproduzcan cada una de las 11 figuras posibles.
-
Si desea hacerlo digitalmente, a través de teléfonos celulares, tabletas o computadora, escanee o pulse sobre el código QR.

EDUCACIÓN SECUNDARIA
-
Realice la construcción del tangrama usando hojas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
A modo de desafío, pida que los estudiantes encuentren la configuración adecuada par obtener cada una de las 6 figuras que se muestran en fondo azul.

CASO 2
Cuando a=b
EDUCACIÓN MEDIA SUPERIOR
-
Realice la construcción del tangrama usando hojas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
Reproduzca cada una de las 5 figuras faltantes que se muestran en fondo azul.
-
En plenaria, pida a los estudiantes que argumenten si el perímetro o el área cambia de una a otra de las 5 figuras posibles.
-
Solicite que a partir de las medidas esablecidas, expresen el área y perímetor de cada figura posible. (La solución se muestra en la siguiente imagen)
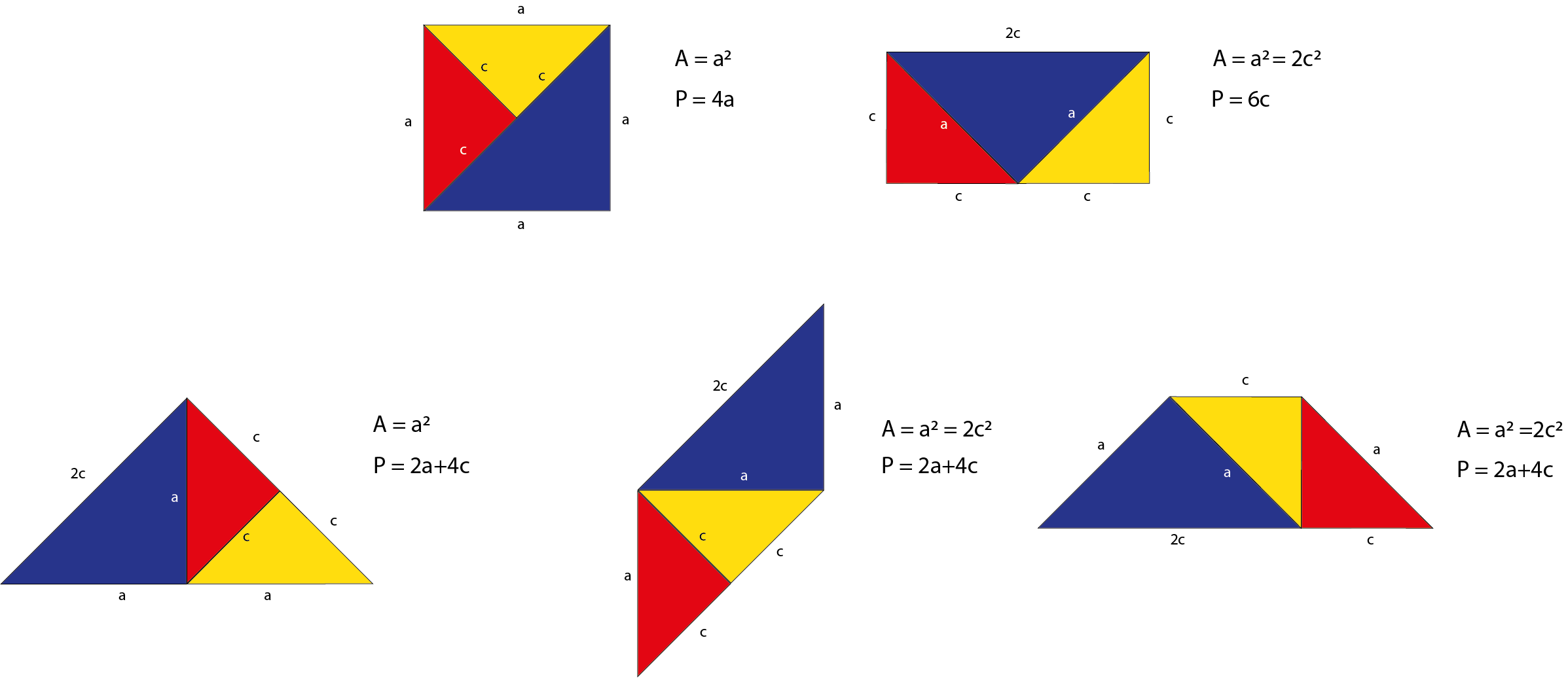
COMO USARLO EN EL AULA
EDUCACIÓN PRIMARIA
-
Realice la construcción del tangrama usando hojas cuadradas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
Pida a los estudiantes que reproduzcan cada una de las 5 figuras posibles.
-
Si desea hacerlo digitalmente, a través de teléfonos celulares, tabletas o computadora, escanee o pulse sobre el código QR.

EDUCACIÓN SECUNDARIA
-
Realice la construcción del tangrama usando hojas cuadradas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
A modo de desafío, pida que los estudiantes encuentren la configuración adecuada par obtener cada una de las 5 figuras que se muestran en fondo azul.


CASO 3
Cuando b=c
COMO USARLO EN EL AULA
EDUCACIÓN PRIMARIA
-
Realice la construcción del tangrama usando hojas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
Pida a los estudiantes que reproduzcan cada una de las 11 figuras posibles y que determinen el número de lados de cada figura.
-
Si desea hacerlo digitalmente, a través de teléfonos celulares, tabletas o computadora, escanee o pulse sobre el código QR.
EDUCACIÓN SECUNDARIA
-
Realice la construcción del tangrama usando hojas cuadradas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
A modo de desafío, pida que los estudiantes encuentren la configuración adecuada par obtener cada una de las 6 figuras que se muestran en fondo azul.
EDUCACIÓN MEDIA SUPERIOR
-
Realice la construcción del tangrama usando hojas de color. Los estudiantes podrán intercambiar las piezas para que tengan un tangrama de tres colores.
-
Reproduzca cada una de las 6 figuras faltantes que se muestran en fondo azul.



El tangrama mínimo de Brügner
Es un tangrama diseñado por el matemático alemán George Brügner en 1984, conformado por tres triángulos rectángulos semejantes.
Una construcción con fines didácticos puede se a partir de una hoja de papel en donde se traza una de sus diagonales y una perpendicular a ella que pase por el lado opuesto.

Tres casos
a, b, c, d, e son diferentes entre sí

El problema consiste en determinar en cuál de los tres casos se obtiene el número máximo de posibles figuras covexas, usando simultáneamente las tres piezas.
a=b

b=c


El tangrama
Brügner propone el análsis a partir de la diagonal de longitud 1

